Learn to moonwalk with waterflow problem

There is an interesting problem called Trapping Rain Water. There are also a lot of truly brilliant solutions of this problem in Chris Done blogpost. But I’d like to find my own solution that would be composable, readable and involve effects.

Trapping Rain Water

We will represent the heights of walls as a list of integers:

type Height = Int

walls :: [Height]
walls = [2,5,1,2,3,4,7,7,6]

To compute the volume of water for each wall, we should know three things:

1. Height of current wall
2. Left peak height
3. Right peak height

We take a lowest of left and right peak heights, subtract minimal peak height from the current wall’s height and voila - we have a volume of trapped water. Let’s take a look on this on an small example:

Let’s imagine that we need to compute a volume of water for b wall. Left peak height (a) = 3, right peak height (c) = 2. Because right wall is lower than left one, water will flow over right wall. So, the volume of water for b wall:

min (height a) (height c) - height b = 2 - 1 = 1

Let’s start from computation the left peak height for every wall with State effect:

type Volume = Int

-- | Choose the highest from previous and current walls:
themax :: Height -> State Height Height
themax h = modify (max h) *> get

-- |  Traverse a list of wall heights with and compute left peak heights:
highest_left :: [Height] -> [Height]
highest_left walls = evalState (traverse themax walls) 0

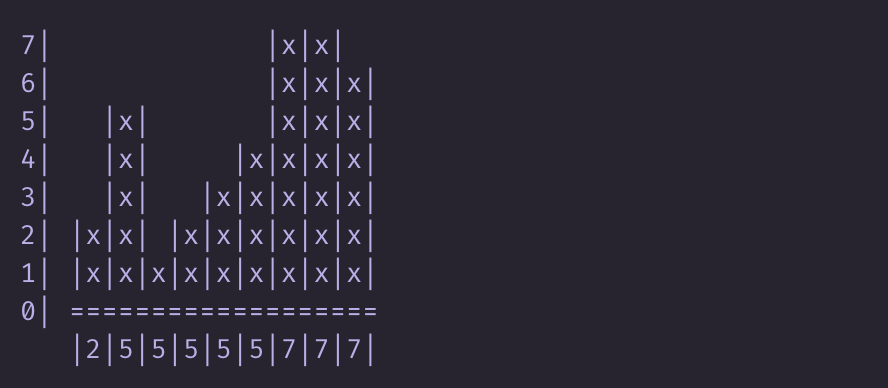
Okay, now we need to compute the right peak heights for all walls, but this time we have to move from right to the left. What we gonna do? Just to reverse a list? There is a more interesting way.

Backwards applicative and Reverse traversable functors

There is an interesting type called Backwards that let you run applicative effects in reverse order:

newtype Backwards f a = Backwards { forwards :: f a }

How does it work? Let’s take a look closer at Backwards’s Applicative instance:

-- | Actually it's a simplified code after replacing liftA2 и <**>
instance Applicative t => Applicative (Backwards t) where
    pure = Backwards . pure
    Backwards f <*> Backwards x = Backwards ((&) <$> x <*> f)

Operator & do the same work as $ (function application) but with different order of parameters: argument first, function second:

f $ x = x & f

Due to laziness, we evaluate the second part of applicative sequence first and the first last. So we evaluate effects in reverse order and apply arguments to an effectful function as usual.

In transformers package there is also a type called Reverse:

newtype Reverse f a = Reverse { getReverse :: f a }

Reverse runs Traversable effect in reverse order using Backwards applicative:

instance (Traversable f) => Traversable (Reverse f) where
    traverse f (Reverse t) = fmap Reverse . forwards $ traverse (Backwards . f) t

Finally, learn to moonwalk

The moonwalk is a dance move in which the dancer moves backwards.

We’re gonna make this trick happen: we will use that themax effectfull function as we move from left to right. But this time we will go from right to left:

themax :: Height -> State Height Height
themax h = modify (max h) *> get

highest_right :: [Height] -> [Height]
highest_right walls = getReverse $ evalState (traverse themax $ Reverse walls)

Now we have everything to compute a volume of water per each wall:

walls = [2,5,1,2,3,4,7,7,6]
let hls = highest_left walls = [2,5,5,5,5,5,7,7,7]
let hrs = highest_right walls = [7,7,7,7,7,7,7,7,6]
zipWith3 (\l x r -> min l r - x) hls walls hrs

You can find source code of this solution here.