In this article I’m going to show you what are adjoint functors about through real programming examples. We will build a lot of useful stuff just with two simplest constructions: an arrow and a comma.

I will deliberately avoid full definitions, axioms, proofs of category theory - I don’t want to copy text from Wikipedia or books. But if you really want to understand these concepts, I strongly recommend this blog cause it helped me a lot. I want to show you how related programming constructions via math abstractions. And there will be Haskell code.

Functions and tuples

Let’s start from simple constructions that should exist in all general-purpose languages.

What is a function? It’s a map between two sets, it’s a code which takes some argument s and returns some result a: s -> a.

What is a tuple? It’s an elementary product of any two types s and a: (s, a).

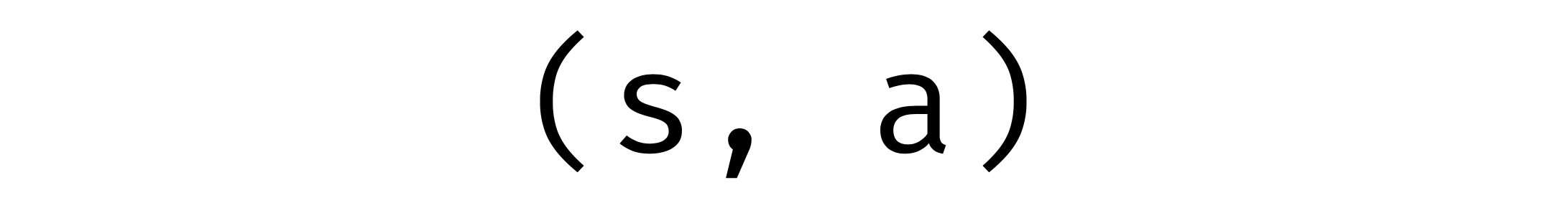
We get used to looking at these two constructions as infix expressions. What if we change our point of view and look at them as prefix expressions? In other words, we pull out operands after the operator.

Now we see that they are pretty similar! They take two arguments in the same order. But there is a difference: the first argument of an arrow (s) is in a negative position, but the first argument of a tuple (s) is in positive (which makes an arrow profunctor and a comma bifunctor). So let’s just ignore those two arguments and just fix them:

Now they are covariant functors and, also they are in such an interesting relation as adjunction!

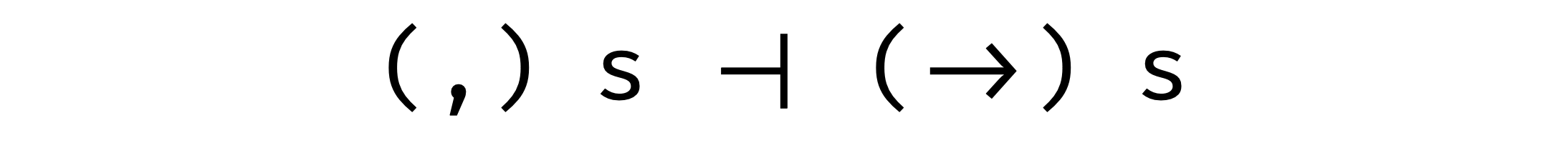
But let’s take one thing at a time.

Categories, functors, adjunctions

A category is a set of objects and arrows:

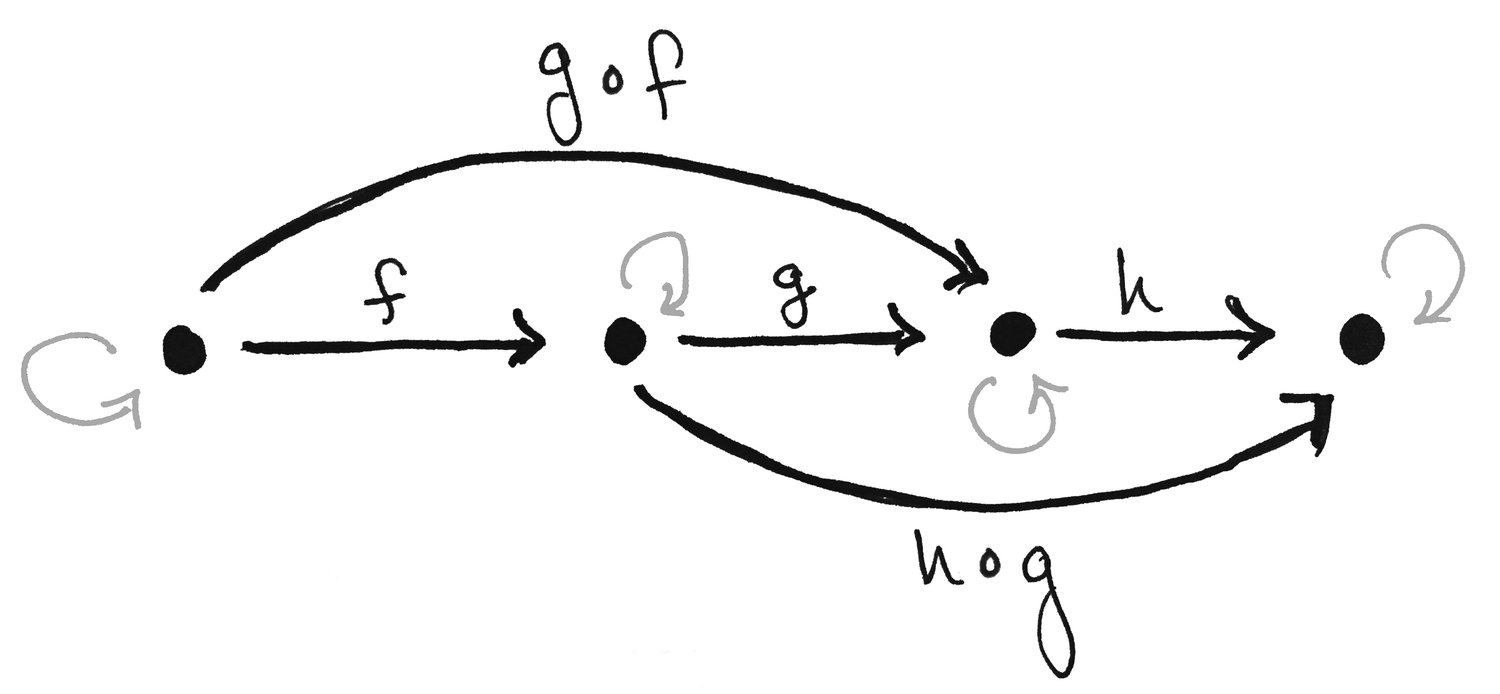«What is a Category? Definition and Examples» © Math3ma

Functors are maps between categories:

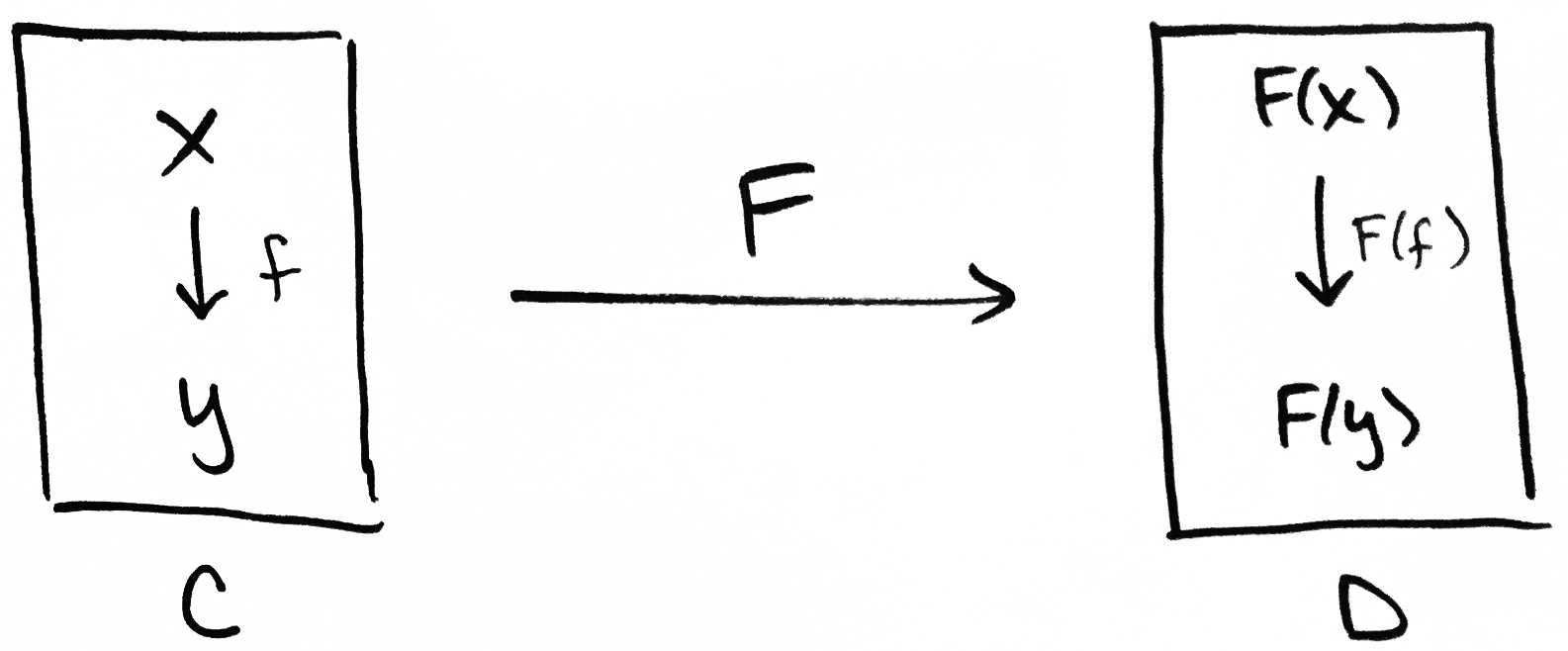«What is a Functor? Definition and Examples, Part 1» © Math3ma/

Adjunction is a special relation between functors. That’s it if we can build two such commutative diagrams and all equations hold, then we can say that F and G are adjoint functors (F ⊣ G):

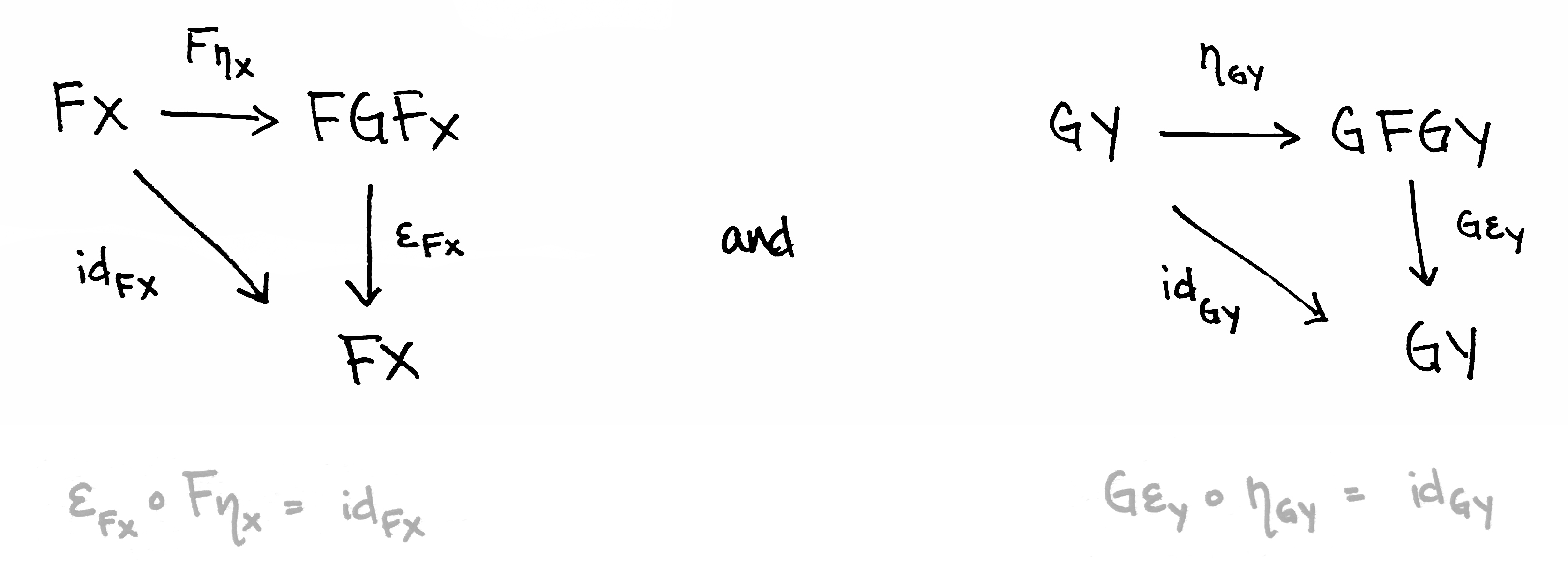«What is an Adjunction? Part 2 (Definition)» © Math3ma

Maybe it looks pretty complicated now but as soon as we get used to these concepts in practice we will make sure that this is not so.

Adjunction of a comma and an arrow

This is how Functor definition usually looks like in languages with parametric polymorphism:

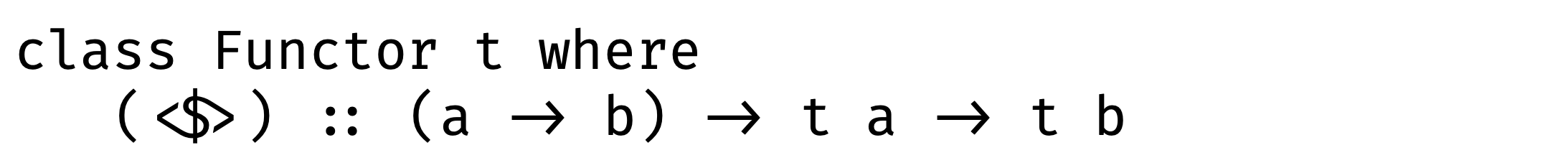
In the case of a tuple, the first argument is fixed therefore we can change only the second one with function:

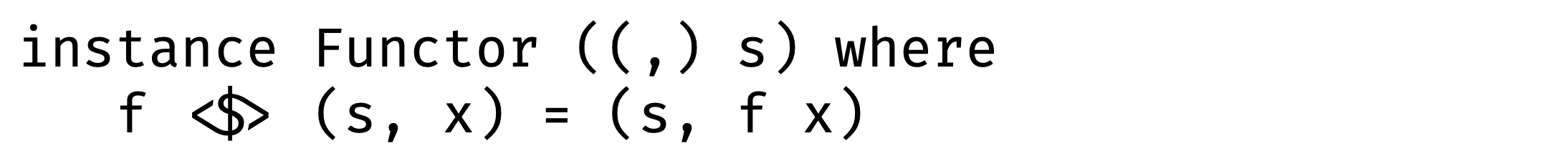
In the case of a function, fmap definition is just a function composition:

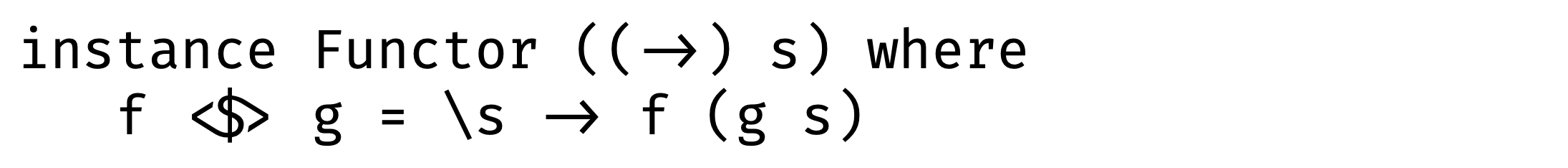
Now it’s time to define adjunction between tuple and function and … it looks pretty complicated.

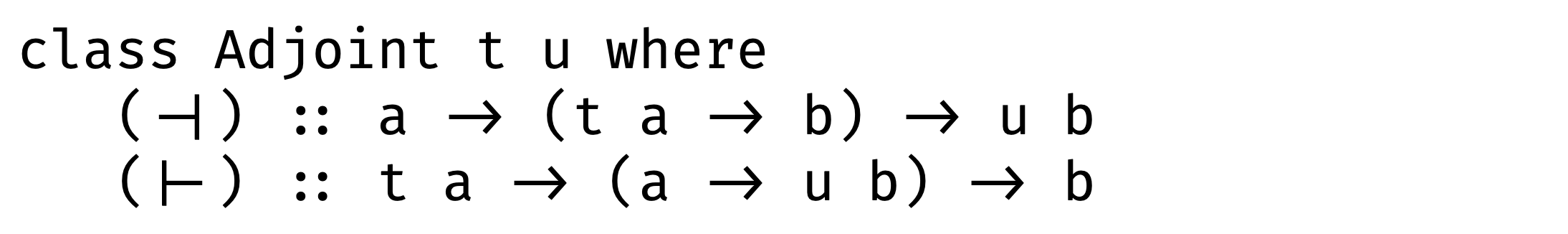
So instead of these methods, let’s define something simpler - unit and counit. Do you remember those two commutative diagrams? Morphism ε corresponds to counit and morphism η corresponds to unit:

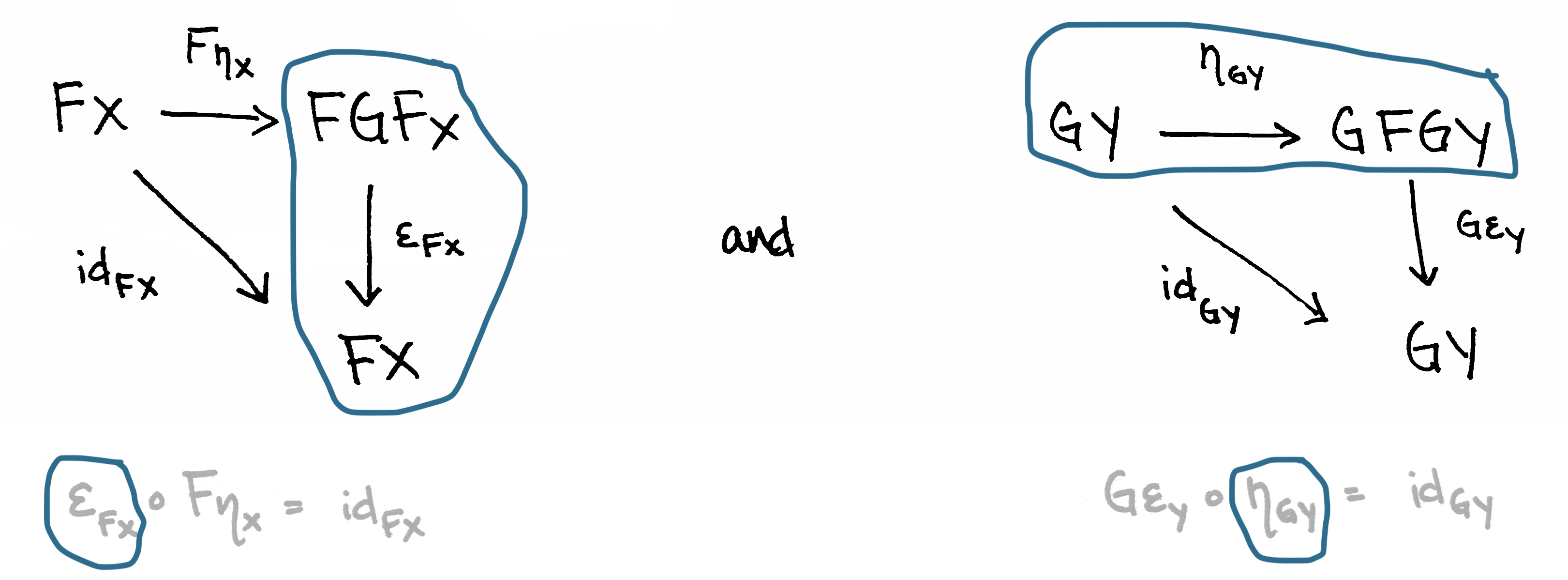«What is an Adjunction? Part 2 (Definition)» © Math3ma

Let’s start from counit:

ε :: f (g a) -> a
-- Replace f and g with comma and arrow:
ε :: (((,) s) ((->) s a)) -> a
-- Disclose parentheses for comma - from prefix to infix:
ε :: (s, ((->) s a)) -> a
-- Disclose parentheses for arrow - from prefix to infix:
ε :: (s, s -> a) -> a

What we got here? counit for a comma and an arrow takes some argument s and function from s to a. Looks like a function application!

ε :: (s, s -> a) -> a
ε (x, f) = f x

Now it’s turn for unit:

η :: a -> g (f a)
-- Replace f and g with comma and arrow:
η :: a -> ((->) s ((,) s a))
-- Disclose parentheses for arrow - from prefix to infix:
η :: a -> s -> ((,) s a)
-- Disclose parentheses for comma - from prefix to infix:
η :: a -> s -> (s, a)

So unit takes s and a as arguments and build a tuple from them:

η :: a -> s -> (s, a)
η x s = (s, x)

Now let’s go back to those scary methods:

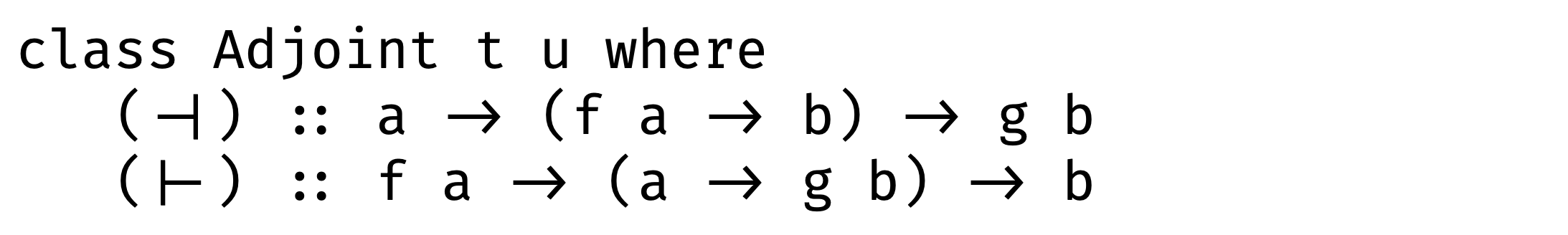
And implement left adjunction and right adjunction:

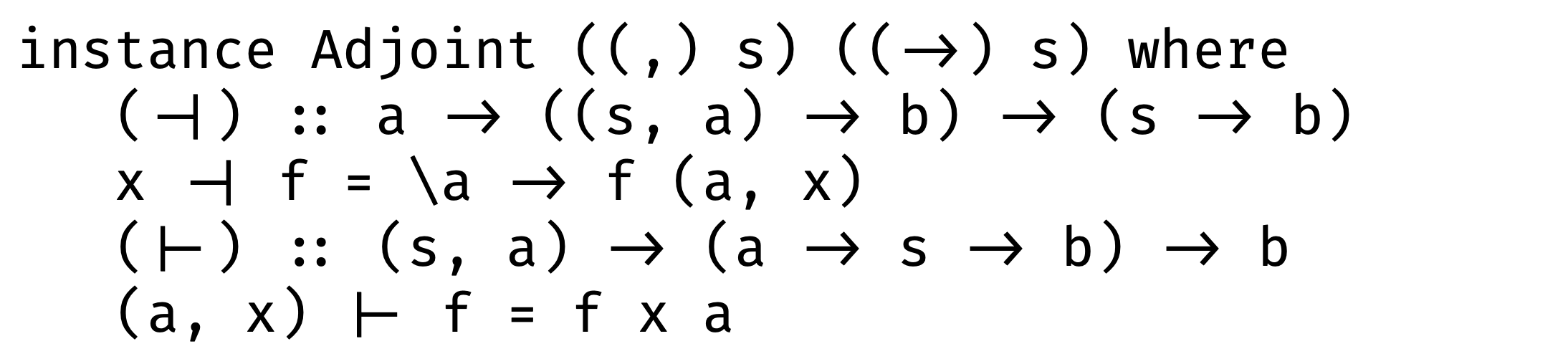
Well, it didn’t get any easier. Sometimes, trying to understand something we have no choice except looking at this very carefully. We can do it now.

Left adjunction: takes a function which takes a tuple ((s, a) -> b ) and as result we have a function which takes a and s as arguments:

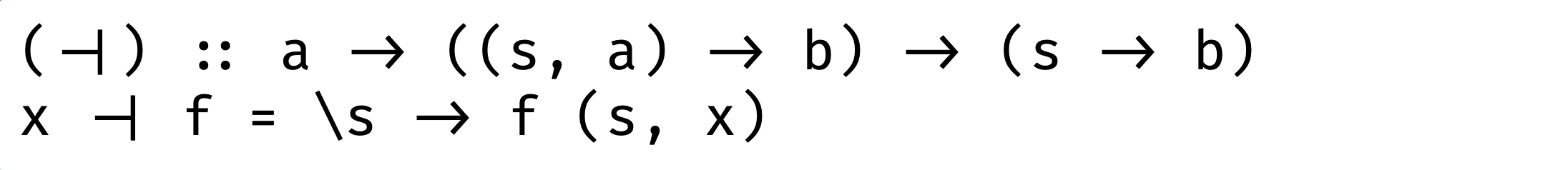
Right adjunction: takes a function which return another function (a -> (s -> b)) and as result we have a function with takes a tuple (s, a):

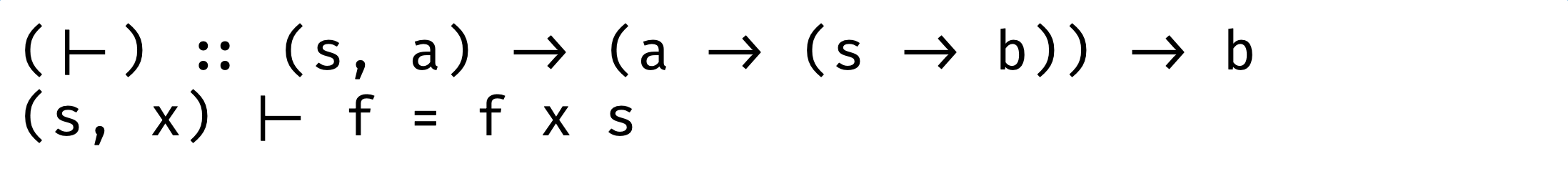
Does this remind you of anything? That is currying!

curry :: ((a, s) -> b) -> a -> s -> b
uncurry :: (a -> s -> b) -> (a, s) -> b

The only difference is the reverse order of arguments

So if you are asked one day ”what is currying” you can answer: ”This is just left adjunction of tuple functor and function functor, what’s the problem?”

Functor combinatorics

There is an idea: let’s try to create a simple functor composition of an arrow and a tuple. Simple functor composition is just wrapping one functor into another one, they are polymorphic over type argument anyway. We can do it in two ways:

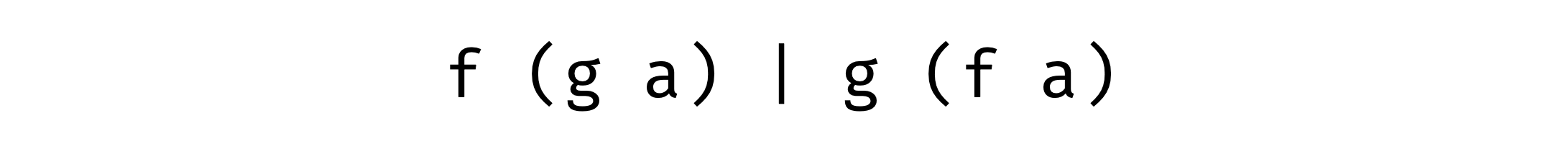
Substitute f and g with comma and arrow (with fixed arguments) accordingly:

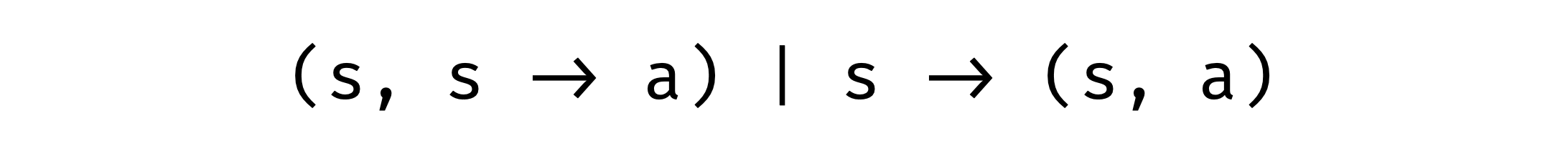
Looks familiar, right? That’s it with the first combination we get Store comonad and with the reverse combination we get State monad:

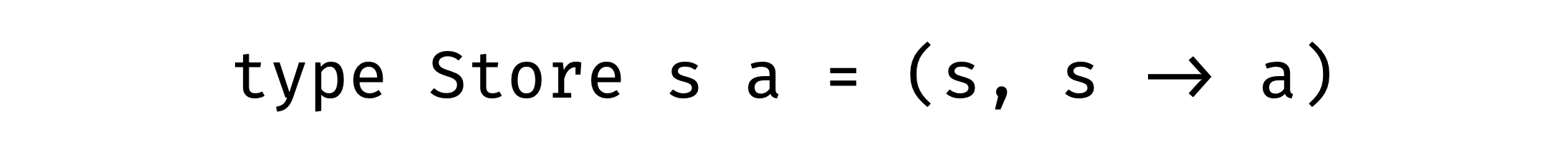
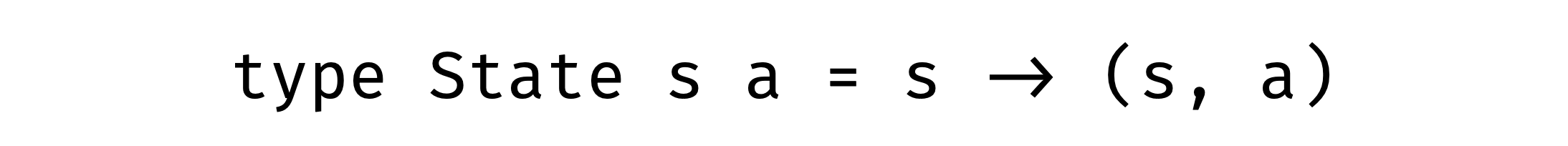
And they are adjoint functors also!

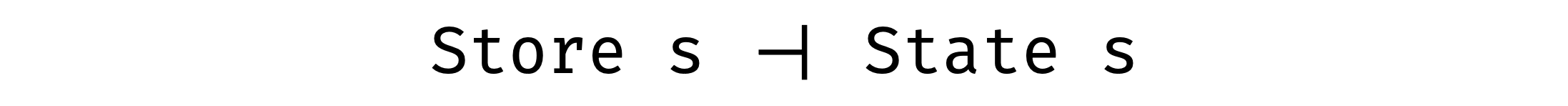
State and Store

What do we think about when we create a program which depends not only on arguments but on some state? Maybe we think about a box where we can put and get something from. Or in the case of finite-state machines, we are focusing on state transitions:

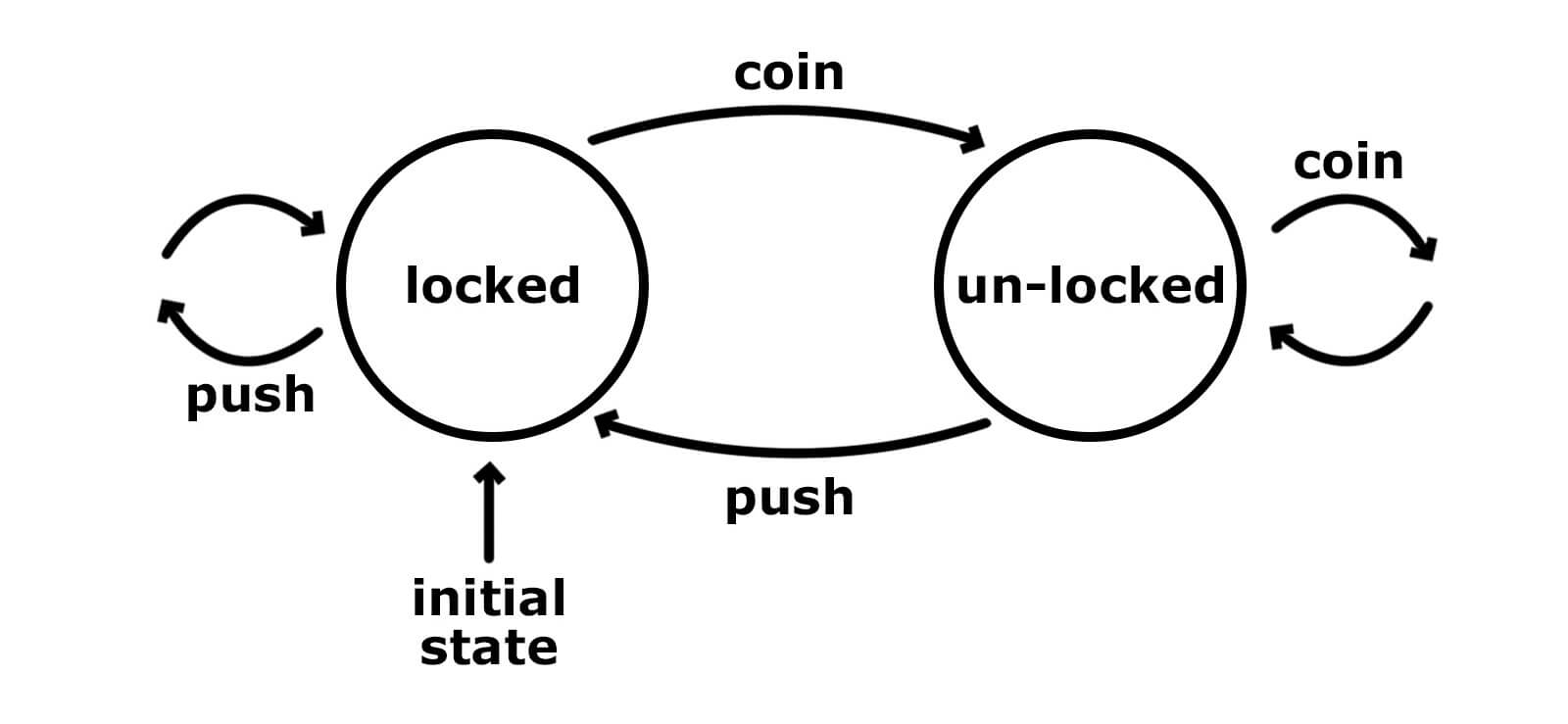
Well, for transitions we have arrows and for a box we have tuple:

type State s a = s -> (s, a)

modify :: (s -> s) -> State s ()
modify f s = (f s, ())

get :: State s s
get s = (s, s)

put :: s -> State s ()
put new _ = (new, ())

Store is something completely different. We store some source s and instruction on how to get a from that s:

type Store s a = (s, s -> a)

pos :: Store s a -> s
pos (s, _) = s

peek :: s -> Store s a -> a
peek s (_, f) = f s

retrofit :: (s -> s) -> Store s a -> Store s a
retrofit g (s, f) = (g s, f)

Where can it be used?

Focusing with lens

Sometimes we have to work with deeply nested data structures, focusing on some details. Imagine you look through a magnifying glass at your data - all other things just disappear from your sight.

And we can construct this magnifying glass with Store comonad:

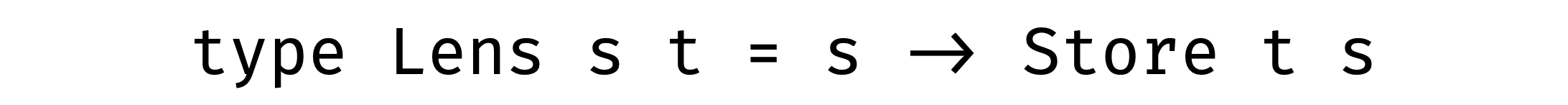
As soon as we can focus on the part of the data we need, we can see what is there, replace this part with new, or modify it with function:

view :: Lens s t -> s -> t
view lens = pos . lens

set :: Lens s t -> t -> s -> s
set lens new = peek new . lens

over :: Lens s t -> (t -> t) -> s -> s
over lens f = extract . retrofit f . lens

Change State with lenses

Let’s use this magic in practice. There was a man:

data Person = Person Name Address (Maybe Job)

We have lenses which can focus on his/her job and address:

job :: Lens Person (Maybe Job)
address :: Lens Person Address

He/she is looking for a job. Some positions have relocation opportunity, depends on the offer he/she takes, he/she needs to move to some city:

hired :: State (Maybe Job) City
relocate :: City -> State Address ()

So we have the effectful hired expression which operates on the state of the current job (Maybe Job). And there is the expression relocate which takes a city as an argument and depends on that city changes Address state. These both effectful expressions operate on some state but we can’t use them together because the type of state is different.

But there is a brilliant zoom function that lets us change the type of state if we have an appropriate lens (it’s pretty similar to lift function in monad transformers).

zoom :: Lens bg ls -> State ls a -> State bg a

We take lenses that we already have and apply them to according expressions:

zoom job hired :: State Person City
zoom address (relocate _) :: State Person ()

… and bind them monadically! Now we have an access to Person state in this combined expression:

zoom job hired >>= zoom address . relocate

You can find those definition sources here.